Василий Грозин
На правах рукописи
Прямая - кратчайший путь между двумя точками. Это каждый знает. Кому не случалось оказываться перед соблазном "срезать угол", пересечь квадратный газон по диагонали и т.п.? Однако не на всех квадратных газонах проложены диагональные тропинки, и мы, люди довольно-таки воспитанные, иногда топаем в обход.
Пространственное мышление - очень полезный навык умственной деятельности. Причем не только для ориентации в трехмерном пространстве, но и глубже - как способ отражения реальности при помощи наглядных геометрических аналогий. Говорим же мы - "прочел книгу по диагонали", "сглаживать противоречия", острота ума, многогранность, даже ассоциации называем параллелями.
Наглядность образов, которые мы используем при общении, играет очень большую роль во взаимопонимании людей. Возьмем хотя бы графики изменения показателей, различные диаграммы, структурные схемы, блок-схемы, карты военных. Все это недаром применяется для объяснения таких непростых предметов, как экономическая деятельность, организованный коллектив, военная операция.
Такая роль наглядности во взаимопонимании людей объясняется тем, что образы пространственных представлений органично связывают теоретическое мышление человека с вещественной реальностью, которая нас окружает. Реальность постоянно напоминает о себе, поддерживает у нас прочность пространственных представлений и их всегдашнюю готовность к применению.
Что касается геометрии, то в ней привычное многообразие форм, размеров, соотношений приобретает строгую математическую упорядоченность, характерную для научного познания и понимания мира. В то же время вездесущие геометрические образы не исчерпывают сегодняшнего знания, а только упорядочивают, структурируют его, облегчают понимание и дальнейшее развитие.
Тем интереснее будет нам вернуться к квадратному газону, который мы хотели бы пересечь по диагонали, но подходящей тропинки не нашли. Нет, лучше пусть это будет городской квартал квадратной формы, там мы уж точно не пройдем напрямик сквозь здания и ограды.

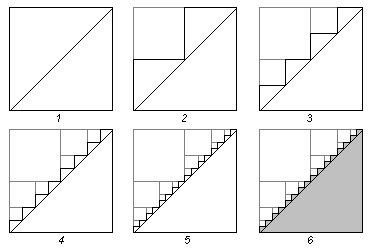
Приближение диагонали квадрата прямоугольными ломаными линиями.
Вспомним немного школьной математики. Путь в обход квартала составит для нас 2L, где L - длина стороны квадрата. А путь по диагонали, если бы он был возможен, составил бы по знаменитой теореме Пифагора √¯2·L ≈ 1,414L. Таким образом, при наличии диагональной дорожки мы можем рассчитывать сократить свой путь почти на 0,586L. Большего геометрическая теория нам предложить не может. Самое смешное, что в сермяжной жизни этот максимум экономии пути никому превзойти не удалось, несмотря на телесказки о параллельных мирах, искривленных пространствах и всяком таком.
Теперь допустим, что между домами квартала есть проход в виде ломаной линии, как изображено в нашей иллюстрации на рисунке номер 2. Если мы пойдем этой дорогой, то угол квадрата срежем, но длина пути все равно останется равной 2L. Ничего странного тут нет, мы же не по диагонали срезали, а просто вывернули срезаемый угол внутрь квадрата.
На рисунке номер 3 мы видим более мелко изломанную линию, которая визуально более похожа на диагональ. Однако длина этой ломаной остается равной 2L. На рисунках 4 и 5 наглядно видно, что с увеличением количества изломов ломаная "стелется" все ближе к диагонали. При большом количестве мелких зубчиков она в изображении буквально сольется с диагональю квадрата. При этом длина мелкозубчатой ломаной линии, как ни странно, ни на йоту не отличается от первоначального обходного пути, то есть, от 2L.
Математики пользуются замечательным понятием предел. Пользуются исключительно успешно, с огромной пользой для науки. В данном случае при увеличении количества изломов наша ломаная визуально приближается к диагонали. Можно сказать, что пределом данной ломаной линии как геометрической фигуры при числе изломов, стремящемся к бесконечности, является диагональ квадрата. За оценку визуального различия двух геометрических фигур можно принять максимум расстояния любой точки одной фигуры до ближайшей точки другой. Этот максимум - высота каждого зубчика - действительно при дроблении ломаной неумолимо стремится к нулю. Стремится к нулю также разница площадей фигуры под ломаной линией (закрашено серым на рисунке номер 6) и треугольника под диагональю.
Но математик про наш случай никогда не скажет, что пределом длины прямоугольной ломаной при количестве изломов, стремящемся к бесконечности, является длина диагонали квадрата. Предел длины ломаной равен 2L, то есть, в точности совпадает с длиной обходного пути. Невероятно: одна из наших сравниваемых фигур очевидным образом стремится к другой и в пределе с ней совпадает. А важнейшая для обеих фигур характеристика - длина - стоит на месте и стабильно отличается от той, что вроде бы должна быть в пределе.
Такие явления, которые при кажущейся очевидности обманывают ожидания человека, принято называть антиинтуитивными.
Еще одним примером антиинтуитивности может служить известный лист Мебиуса.
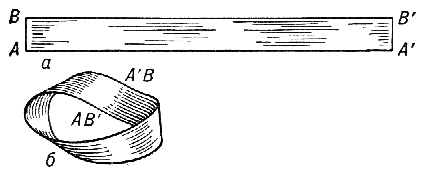
Построение листа Мёбиуса (Рисунок из БСЭ 3-е изд.)
Начать с того, что, если эту полоску (ленточку) бумаги, перегнутую и склеенную в кольцо, разрезать вдоль полосы по осевой линии, то она не распадется на два колечка половинной ширины, как было бы с обычным бумажным кольцом, а вывернется в одно узкое бумажное кольцо с двумя перегибами и удвоенной длины. Предвидеть такой фокус, когда заранее не знаешь ответа, - не каждому по силам.
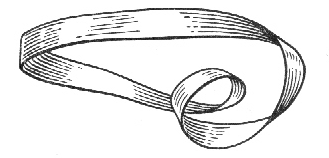
Поверхность, получаемая из листа Мёбиуса разрезанием его
по средней линии (Рисунок из БСЭ 3-е изд.)
Помимо этой первой - иллюзионистской - антиинтуитивности с листом Мебиуса связана и вторая - лингвистическая. Его часто называют реальным примером односторонней поверхности. И это на том лишь основании, что данная фигурка, сделанная из самой обычной двусторонней бумаги, позволяет переходить без отрыва карандаша с одной стороны бумажной ленты на противоположную, не пересекая края ленты. Заметим, противоположная сторона была у ленты до склеивания, и при хитром склеивании она никуда не исчезла, а лишь соединилась с лицевой стороной.
Как понимать двусторонность исходной поверхности до момента хитрой склейки? Как невозможность перейти на ее изнанку, не пересекши края поверхности? А разве недостаточно самого факта наличия противоположной поверхности, то есть, возможности из каждой точки восставить, как выражаются математики, перпендикуляр и с лицевой, и с изнаночной стороны? Именно так двусторонность толкуют сами же математики. И эта двусторонность никуда не исчезает при склейке листа Мебиуса. Поверхность, у которой "лицевая" сторона смыкается с "изнаночной", остается двусторонней поверхностью, только привычная граница между сторонами - край бумажной полоски - в месте склейки устранена путем переворота.
Добро бы математики определяли свою одностороннюю поверхность наподобие внешней границы объемного тела, у которой внутренняя сторона смыкается с толщей материала и по этим соображениям не включается в абстрактное понятие «односторонняя поверхность». Это в жизни всякая палка о двух концах, а математики позволяют себе заводить абстрактные палки об одном конце (луч) и палки конечной длины, но с откушенными концами (интервал). Так почему бы не заиметь безызнаночную поверхность, чисто "внешнюю" без "внутренней"?
Нет, не могут. Или не хотят. Поверхность представляется ими как некая бестелесная оболочка, как тонкая пленка «толщиной в одну бесконечно малую точку», как платье голого короля. И мы, сермяжные, математикам не указ. Но разве мы и лингвистам не указ?
Тот, кто придумал называть лист Мебиуса односторонней поверхностью, произвольно заузил трактовку одно- и двусторонности, свел ее лишь к одному признаку, который почему-то объявлен решающим в данном вопросе, хотя есть и другой признак, потенциально более решающий. Правильно было бы назвать лист Мебиуса «поверхностью с соединенными сторонами». Тогда антиинтуитивность вокруг этой головоломки была бы рассеяна, как она рассеяна в терминах «несходящаяся последовательность», «разрыв непрерывности» и им подобных.
Кстати, сугубые математики отсылают за более точной терминологией определения поверхности в свой раздел «Топология», где сермяжная связь абстракций с реальными примерами уже по-честному разорвана, а термин "односторонняя" заменен на "неориентируемая".
Наш дилетантский экскурс в математику можно было бы счесть шуткой, если бы не параллели со вчерашней и сегодняшней действительностью.
Недавно автор данной статьи готовил для «Музея разрушения СССР« материал 1990 года "Кино тоталитарной эпохи". В этой публикации профессионалы от кинематографа рассматривают в одном общем ряду фильмы муссолиниевской Италии, гитлеровской Германии и сталинского Советского Союза. Чтобы возыметь право на уподобление таких довольно различных, особенно для советских читателей, явлений общественного сознания, участники обсуждения склеивают с переворотом свою собственную "неориентируемую поверхность" - понятие "тоталитарный".
Это антиинтуитивное понятие в последние десятилетия стало привычным благодаря настойчивому употреблению на телевидении, радио, в прессе, политике и обслуживающих последнюю науке и культуре. По-сермяжному оно представляет собой типичную "поверхность со сторонами, которые склеены с переворотом". Главными параметрами жизни общества в этом понятии объявлены многопартийность и рыночность, толкуемые весьма абстрактно и поверхностно.
Людям, разгоряченным перестройкой, не удалось своевременно разгадать стратегических целей тогдашней лингвистической антиинтуитивности. Теперь за новейшей балаганно-кукольной многопартийностью нетрудно увидеть мегапартию сверхчеловеков, дорвавшихся до мирового господства. А за рыночной стихийностью - слаженную игру меньшинства против большинства.
19 мая 2009 г.
Москва
См. также
О различении рациональной и иррациональной
аргументации
Думай, как я
"Толерантность" - презумпция виновности своих
Общечеловеческие ценности в натуре
Память
О самопонимании современного человека